Notice
Recent Posts
Recent Comments
Link
헬창 개발자
[파이썬으로 구현하는 간단한 선형회귀] 본문
1. 선형 회귀란?
선형 회귀(Linear Regression)는 입력 변수와 출력 변수 간의 관계를 선형 함수로 모델링하는 기법입니다. 목표는 입력 변수와 출력 변수 간의 관계를 설명하는 직선(혹은 평면)을 찾는 것입니다. 이 기법은 회귀 분석의 가장 기본적인 형태입니다.
2. 선형 회귀의 수식
단일 입력 변수 xx와 출력 변수 yy에 대한 선형 회귀 모델은 다음과 같은 수식으로 표현됩니다:

- β0는 절편(Intercept)
- β1은 기울기(Slope)
3. 선형 회귀 알고리즘
선형 회귀 알고리즘의 목표는 데이터 포인트와 예측 직선 간의 오차를 최소화하는 것입니다. 오차는 주로 평균 제곱 오차(Mean Squared Error, MSE)로 측정됩니다. 선형 회귀의 주요 단계는 다음과 같습니다
1.모델 정의
2.비용 함수 정의: 일반적으로 평균 제곱 오차(MSE)를 비용 함수로 사용합니다. 비용 함수는 모델의 예측 값과 실제 값 간의 차이를 측정합니다
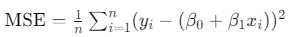
여기서 n은 데이터 포인트의 수, yi는 실제 값, xi는 입력 값입니다.
3.모델 학습: 비용 함수를 최소화하기 위해 경사 하강법(Gradient Descent) 등의 최적화 알고리즘을 사용하여 기울기와 절편을 업데이트합니다.
4.예측 수행: 학습된 모델을 사용하여 새로운 데이터에 대한 예측을 수행합니다.
4. 소스코드
data.txt
6.1101,17.592
5.5277,9.1302
8.5186,13.662
7.0032,11.854
5.8598,6.8233
8.3829,11.886
7.4764,4.3483
8.5781,12
6.4862,6.5987
5.0546,3.8166
5.7107,3.2522
14.164,15.505
5.734,3.1551
8.4084,7.2258
5.6407,0.71618
5.3794,3.5129
6.3654,5.3048
5.1301,0.56077
6.4296,3.6518
7.0708,5.3893
6.1891,3.1386
20.27,21.767
5.4901,4.263
6.3261,5.1875
5.5649,3.0825
18.945,22.638
12.828,13.501
10.957,7.0467
13.176,14.692
22.203,24.147
5.2524,-1.22
6.5894,5.9966
9.2482,12.134
5.8918,1.8495
8.2111,6.5426
7.9334,4.5623
8.0959,4.1164
5.6063,3.3928
12.836,10.117
6.3534,5.4974
5.4069,0.55657
6.8825,3.9115
11.708,5.3854
5.7737,2.4406
7.8247,6.7318
7.0931,1.0463
5.0702,5.1337
5.8014,1.844
11.7,8.0043
5.5416,1.0179
7.5402,6.7504
5.3077,1.8396
7.4239,4.2885
7.6031,4.9981
6.3328,1.4233
6.3589,-1.4211
6.2742,2.4756
5.6397,4.6042
9.3102,3.9624
9.4536,5.4141
8.8254,5.1694
5.1793,-0.74279
21.279,17.929
14.908,12.054
18.959,17.054
7.2182,4.8852
8.2951,5.7442
10.236,7.7754
5.4994,1.0173
20.341,20.992
10.136,6.6799
7.3345,4.0259
6.0062,1.2784
7.2259,3.3411
5.0269,-2.6807
6.5479,0.29678
7.5386,3.8845
5.0365,5.7014
10.274,6.7526
5.1077,2.0576
5.7292,0.47953
5.1884,0.20421
6.3557,0.67861
9.7687,7.5435
6.5159,5.3436
8.5172,4.2415
9.1802,6.7981
6.002,0.92695
5.5204,0.152
5.0594,2.8214
5.7077,1.8451
7.6366,4.2959
5.8707,7.2029
5.3054,1.9869
8.2934,0.14454
13.394,9.0551
5.4369,0.61705소스코드
import numpy as np
import matplotlib.pyplot as plt
path= "C:/Users/whcks/Desktop/ex1data.txt"
f = open(path, 'r')
test = f.readlines()
x=[]
y=[]
a=[]
for i in test: # 데이터 분류
i.strip('\n')
a=i.split(',')
x.append(float(a[0]))
y.append(float(a[1]))
x_train=np.array(x) # 훈련 데이터
y_train=np.array(y) # 정답 데이터
W,b=0,0
learning_rate = 0.01 # 학습률
epochs = 1000 # 반복횟수
n_data = float(len(x))
for j in range(epochs):
y_pred = x_train * W + b # 예측값
cost = np.sum((y_pred - y_train) ** 2) / n_data # 손실 함수
gradient_w = np.sum(x_train*(y_pred- y_train))/ n_data
gradient_b = np.sum(y_pred - y_train) / n_data
W -= learning_rate * gradient_w #경사하강법
b -= learning_rate * gradient_b
if(j%100==0):
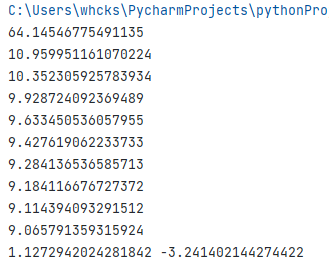
print(cost) #오차 출력
y_pred = W*x_train + b #학습된 선형함수
print(W, b) # 학습된 가중치와 편향(계수와 절편)
plt.scatter(x_train,y_train)
plt.plot(x,y_pred, color="red")
plt.show()결과화면

'공부방' 카테고리의 다른 글
| Node.js 첫걸음 (0) | 2022.07.26 |
|---|---|
| [운영체제] 프로세스란????????????????????? (0) | 2022.04.24 |
| 백준 15781번 헬멧과 조끼 : 파이썬 (0) | 2021.12.29 |
| 파이썬으로 구현하는 머신러닝 (1) | 2021.12.24 |
| 학사 관리 시스템 ER모델링 (2) | 2021.10.17 |




