헬창 개발자
그래프 브릿지 찾기 : 파이썬 본문
브릿지란 단절선, 절단선을 의미하며 그래프가 2개로 나눠지는 간선을 의미한다.

다음과 같은 그래프가 있다. 이 그래프에 단절선은 어떻게 찾을까??
우리가 필요한 자료구조는
순회 체크 리스트, 현재 정점, 부모 정점, 브리지를 담을 리스트, 우회로 변수, (a, b) = (본인 순번, 주변 최소 순번)이다.
이제 알고리즘을 살펴보자
요약은 다음과 같다.
# 자식 노드에서 부모 노드로 역으로는 검사 불가
(a, b)=(순번, 주변 최소 순번)를 비교하여 탐색하고 자식 노드의 b가 부모 노드의 a와 같으면 다른 노드를 통해 부모로 갈 수 있기 때문에 우회로가 있다고 판단하여 브리지가 아니게 되고 자식 노드의 b가 부모 노드의 a 보다 크면 우회로가 없기 때문에 브리지라고 판단한다.

정점 1에서 탐색을 시작한다고 하자, 그러면 순번 1번을 받고 주변 노드의 순번을 비교하여 작은 값을 가진다.
이후 정점 1의 부모는 현재 없고 자식은 순번 기준으로 2를 탐색한다.

(a, b) = (본인 순번, 주변 최소 순번)
정점 2는 정점 1에서 왔고 주변 정점과 순번을 비교하여 (2,2) 값을 가진다.
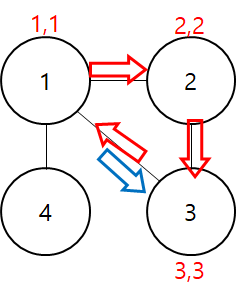
1 -> 2 -> 3 순회가 끝나고 3->1 순회를 시작하는데 3번을 통해서 1번으로 가는 우회로가 존재하기 때문에
정점 3번은 주변 최소 순번 1을 가진다.

정점 2도 정점 3을 통해서 정점 1로 갈 수 있기 때문에 주변 최소 순번 1을 반환받는다.

최종 부모 노드였던 정점 1은 주변 자식들이 가지는 최소 순번이 본인과 같기 때문에 우회로가 있다 판단하여 브리지가 없다고 결론을 내린다.
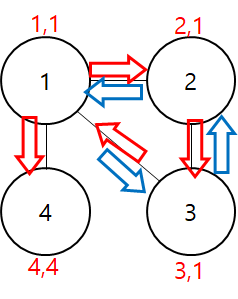
이제 정점 4에 대해서 탐색을 시작하고 정점 4는 주변 최소 순번이 부모의 순번을 제외하고는 없어서 (4,4)를 반환한다.

정점 1에서 출발한 정점 4를 비교했을 때 주변 최소 순번이 부모인 정점 1보다 크므로 우회로가 없다 판단하여 해당 간선을 브리지라고 판단하여 추가한다.
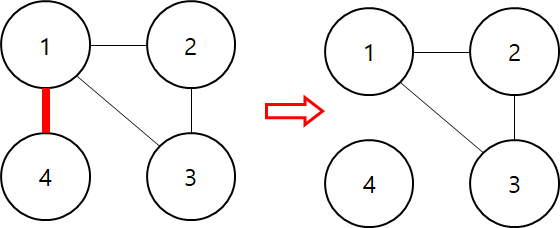
(1,4) 간선을 제거하면 그래프가 나뉘는 걸 확인이 가능하다.
코드
from collections import defaultdict
def dfs(here, parent):
global cnt
cnt += 1
order[here] = cnt
ret = order[here]
for next in graph[here] :
if next == parent : # 역으로 가는건 무시
continue
if order[next] : # 방문한적 있으면
ret = min(ret, order[next])
continue
subtree = dfs(next, here)
ret = min(subtree, ret)
# 부모로 바로가는 간선(현재간선)을 제외하고 서브트리의 간선 중 부모보다 선조로 갈 수 없으면
if subtree > order[here] :
cutEdge.add(tuple(sorted([here,next])))
return ret
# N개
V,E = map(int, input().split())
graph = defaultdict(set)
cutEdge = set()
candidates = set()
for _ in range(E) :
a,b = map(int, input().split())
graph[a].add(b)
graph[b].add(a)
candidates.add(a)
candidates.add(b)
order = [None] * (V+1) #순회 체크 리스트
cnt = 0
dfs(1, None) # 정점 1부터 시작
print(len(cutEdge))
for a,b in cutEdge :
print(a,b)결과 화면

'자료구조' 카테고리의 다른 글
| AVL 트리 구현 : 파이썬 (5) | 2021.09.07 |
|---|---|
| 해시 함수 : 파이썬 (2) | 2021.08.12 |
| 큐를 이용한 은행 업무 시스템 : 파이썬 (1) | 2021.07.30 |
| 스택을 이용한 후위 표기, 연산 : 파이썬 (0) | 2021.07.29 |
| 이진 트리를 이용한 연락처 프로그램 : C언어 (0) | 2021.07.28 |



